[C++] 힙 & 힙 정렬(Heap & Heap Sort)

힙(Heap)

• 히프는 완전이진트리 기반 자료구조이다.
• 여러 개의 값들 중에서 가장 큰 값이나 가장 작은 값을 빠르게 찾아내도록 만들어진 자료구조이다.
• 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰 이진트리를 뜻한다.
• key(부모노드) ≥ key(자식노드) 조건을 항상 성립한다.
• 노드의 인덱스
  • 배열로 구현 시 0번째 인덱스가 아니라 1번째 인덱스에서부터 시작된다.
  • 왼쪽 자식의 인덱스 = (부모의 인덱스) * 2
  • 오른쪽 자식의 인덱스 = (부모의 인덱스) * 2 + 1
  • 부모의 인덱스 = (자식의 인덱스) / 2

 

힙 트리

 

힙 트리

 

힙 트리는 중복된 값을 허용한다.

 

힙 트리가 아닌 예

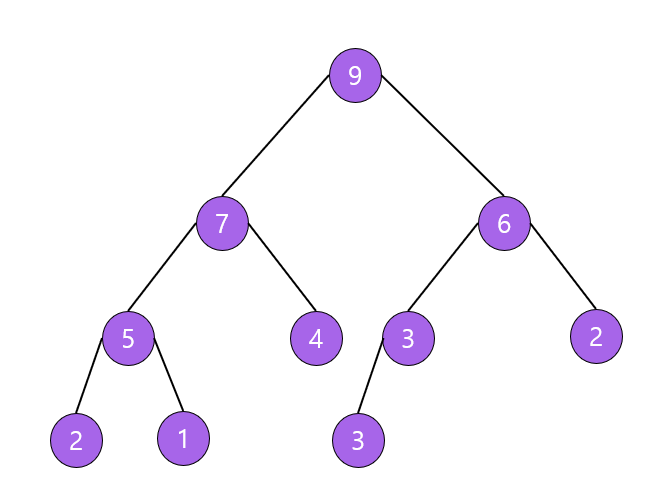
완전 이진 트리가 아니기 때문에 힙 트리는 아니다.

 

힙 종류

최대 힙(max heap)

• 부모 노드의 키값이 자식 노드의 키값보다 크거나 같은 완전 이진 트리
• key(부모 노드) ≥ key(자식 노드)

최대 힙

 

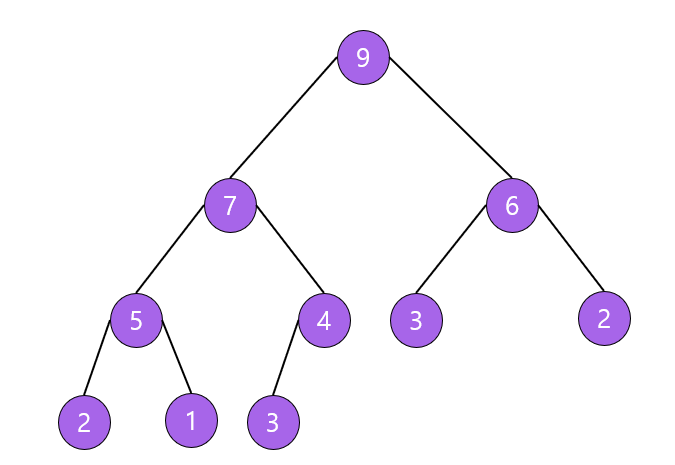
최소 힙(min heap)

• 부모 노드의 키값이 자식 노드의 키값보다 작거나 같은 완전 이진 트리
• key(부모 노드) ≤ key(자식 노드)

최소 힙

 

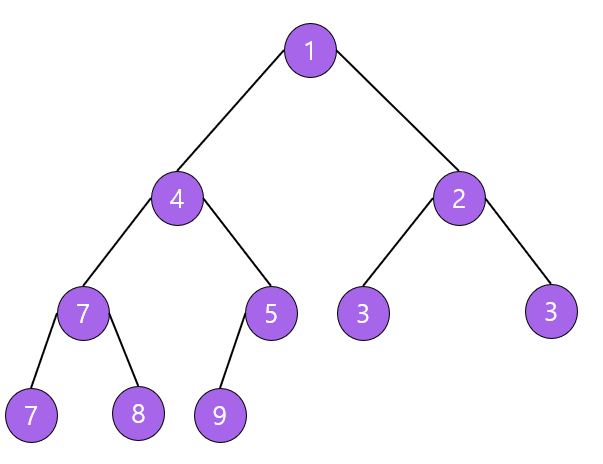
힙 정렬

• 최대 힙을 이용하면 정렬이 가능하다.
• 시간 복잡도: O(nlogn)
• 불안정 정렬이다.
• 과정
  • 최대 힙을 구성
    • 루트를 힙의 마지막 원소와 교환한다.
    • 마지막 원소를 제외하고 나머지 원소에 대해서 반복한다.
    • 정렬된 원소를 제외하고 최대 힙에 원소가 1개 남으면 정렬을 종료한다.

 

힙 삽입

힙 삽입 순서

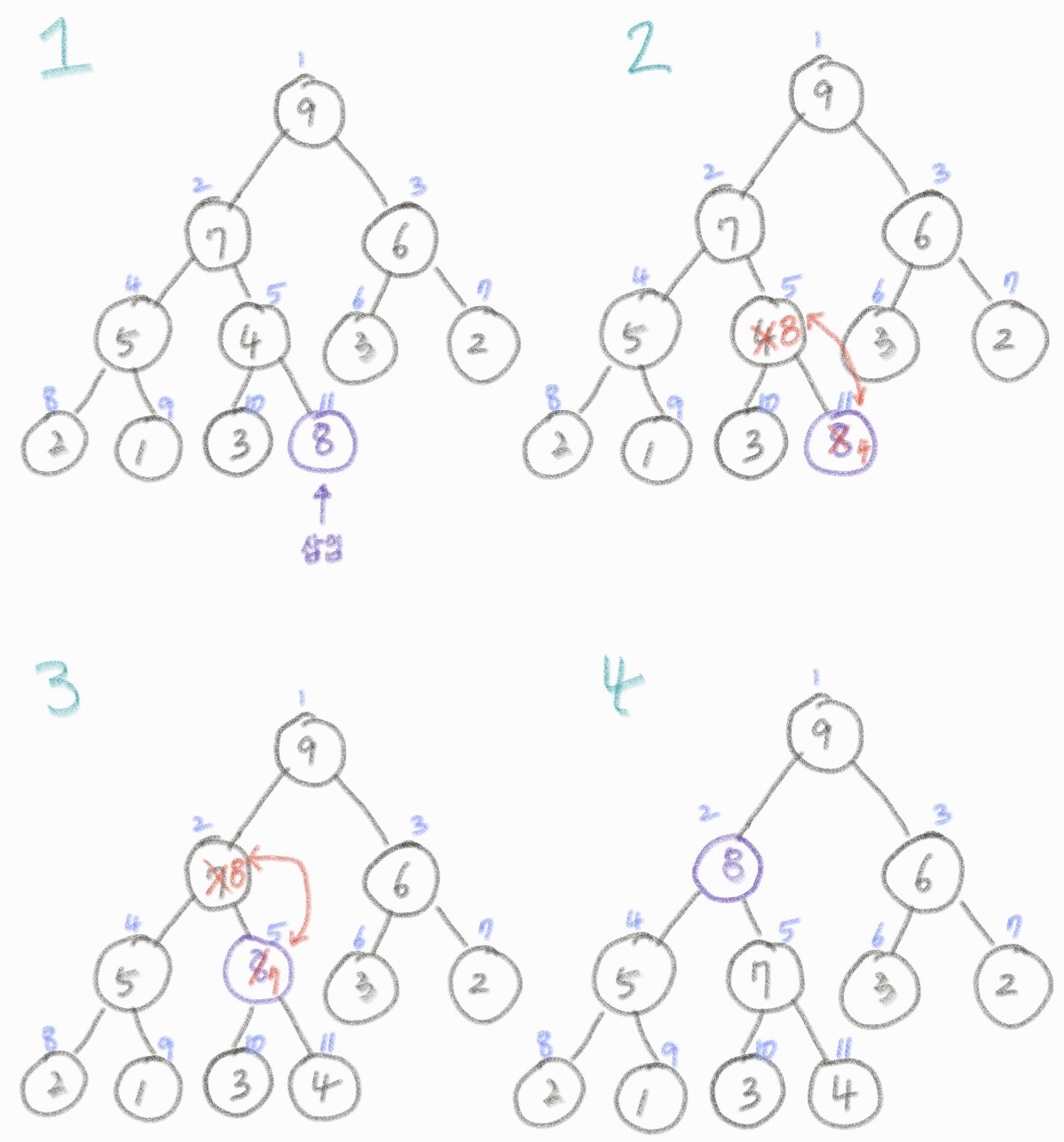
• 새로운 노드를 힙의 가장 마지막 노드로 삽입하고, 부모 노드와 비교하여 히프의 성질을 만족시켜 주어야 한다.

 

힙 삭제

힙 삭제

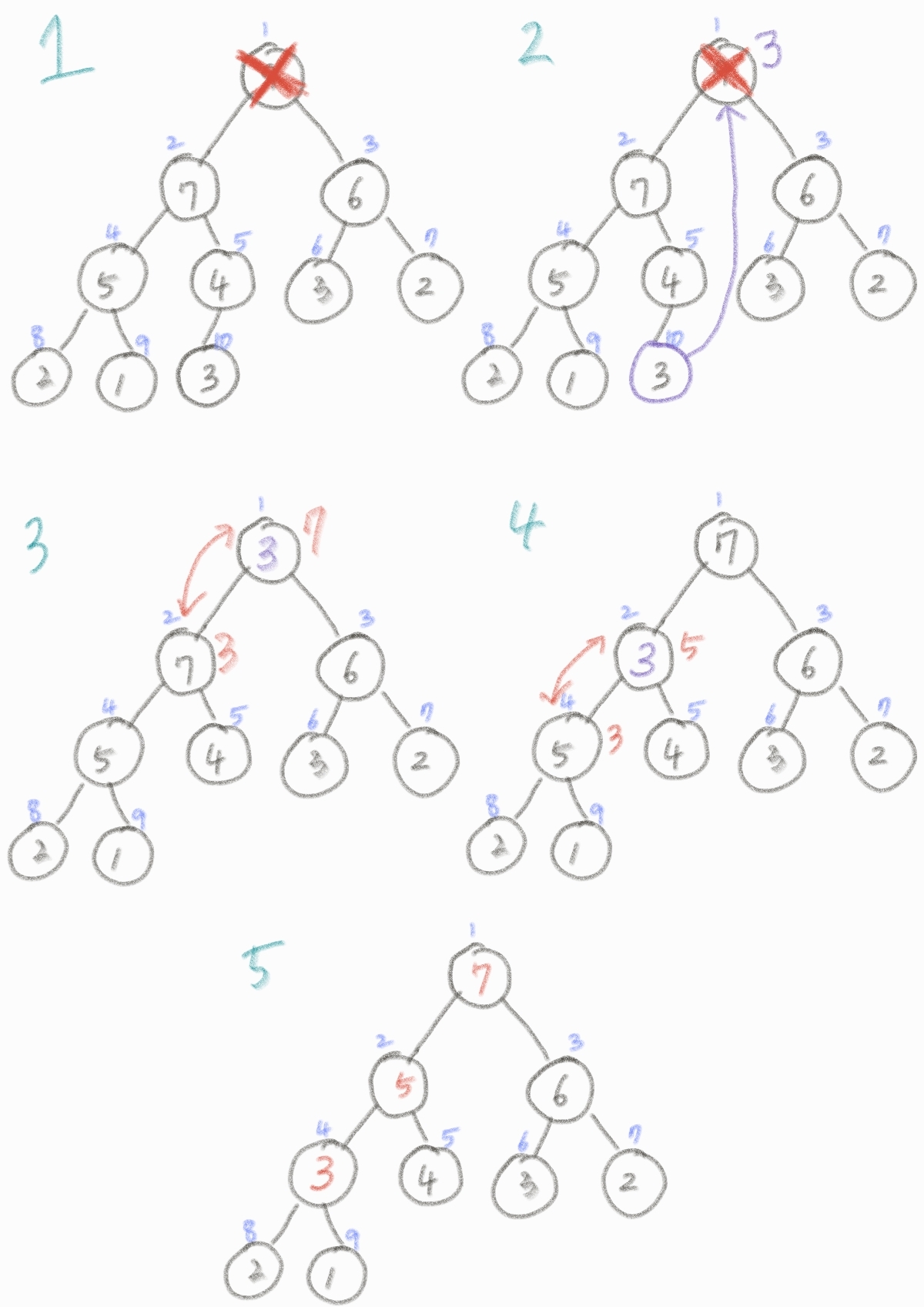
• 최대 값을 가진 요소를 제일 먼저 삭제한다. (즉 루트 노드가 삭제)
• 루트 노드를 삭제한 후에 힙의 마지막 노드를 루트 자리에 놓은 후 자식 노드와 크기 비교를 하여 힙의 성질을 만족시킨다.

 

구현

#include <iostream>
#include <stdio.h>

using namespace std;

int n, heap[10000001];

void heapify(int i) {
	int cur = 2 * i;

	if (cur < n && heap[cur] < heap[cur + 1]) cur++;

	if (heap[i] < heap[cur]) {
		swap(heap[i], heap[cur]);
		if (cur <= n / 2)
			heapify(cur);
	}
}

void heapsort(int i) {
	swap(heap[1], heap[i]);

	int root = 1; // 배열의 1번을 루트로 설정
	int cur = 2;

	while (cur / 2 < i) {
		cur = 2 * root;
		if (cur < i - 1 && heap[cur] < heap[cur + 1]) cur++;
		if (cur < i&& heap[root] < heap[cur])
			swap(heap[root], heap[cur]);
		root = cur;
	}
}

int main() {
	cout << "정렬할 숫자 입력: ";
	scanf_s("%d", &n);
	for (int i = 1; i <= n; i++) {
		cout << "정수 입력:";
		scanf_s("%d", &heap[i]);
	}

	for (int i = n / 2; i > 0; i--) // 최초 heap 생성
		heapify(i);

	for (int i = n; i > 0; i--) // heap 정렬
		heapsort(i);

	for (int j = 1; j <= n; j++) // 출력
		cout << heap[j] << " ";
}

 

 

참고 자료